还有不到40天就到了2016考研初试的时间了，为了让学生能够更好地应对考研，本文将讨论一下中值定理这块的相应证明题的一般解题思路。

中值定理这块一直都是很多考生的“灾难区”，一直没有弄清楚看到一个题目到底怎么思考处理，因此也是考研得分比较低的一块内容，如果考生能把中值定理的证明题拿下，那么我们就会比其他没做上的同学要高一个台阶，也可以说这是一套“拉仇恨”的题目。下面跨考教育数学教研室佟老师就和大家来一起分析一下这块内容。

一、具体考点分析

首先我们必须弄清楚这块证明需要的理论基础是什么，相当于我们的工具，那需要哪些工具呢?

第一：闭区间连续函数的性质。

最值定理：闭区间连续函数的必有最大值和最小值。

推论：有界性(闭区间连续函数必有界)。

介值定理：闭区间连续函数在最大值和最小值之间中任意一个数，都可以在区间上找到一点，使得这一点的函数值与之相对应。

零点定理：闭区间连续函数，区间端点函数值符号相异，则区间内必有一点函数值为零。

第二：微分中值定理(一个引理，三个定理)

费马引理：函数f(x)在点ξ的某邻域U(ξ)内有定义，并且在ξ处可导，如果对于任意的x∈U(ξ)，都有f(x)≤f(ξ) (或f(x)≥f(ξ) )，那么f'(ξ)=0。

罗尔定理：如果函数f(x)满足：

(1)在闭区间[a,b]上连续;

(2)在开区间(a,b)内可导;

在区间端点处的函数值相等，即f(a)=f(b)，

那么在(a,b)内至少有一点ξ(a<ξ

柯西中值定理：如果函数f(x)及F(x)满足

(1)在闭区间[a,b]上连续;中文考研网

(2)在开区间(a,b)内可导;

(3)对任一x∈(a,b)，F'(x)≠0

那么在(a,b) 内至少有一点ξ，使等式[f(b)-f(a)]/[F(b)-F(a)]=f'(ξ)/F'(ξ)成立。

第三：积分中值定理：

如果函数 f(x) 在积分区间[a, b]上连续，则在 [a, b]上至少存在一个点 ξ，使下式成立

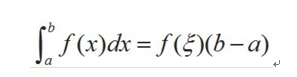
加强版：如果函数 f(x) 在积分区间[a, b]上连续，则在 (a, b)上至少存在一个点 ξ，使下式成立

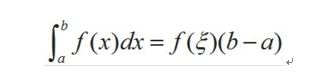
第四：变限积分求导定理： 如果函数f(x)在区间[a，b]上连续，则积分变上限函数在[a,b]上具有导数，并且导数为：

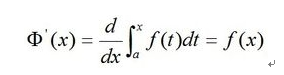
第五：牛顿--莱布尼茨公式：如果函数f(x) 在区间[a,b] 上连续，并且存在原函数F(x) ，则

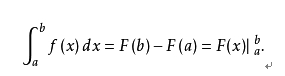
以上定理要求理解并掌握定理内容和相应证明过程。

二、注意事项

针对上文中具体的考点，佟老师再给出几点注意事项，这几个注意事项也是在证明题中的“小信号”，希望大家理解清楚并掌握：

1. 所有定理中只有介值定理和积分中值定理中的ξ所属区间是闭区间。

2. 拉格朗日中值定理是函数f(x)与导函数f'(x)之间的桥梁。

3. 积分中值定理是定积分与函数之间的桥梁。

4. 罗尔定理和拉格朗日中值定理处理的对象是一个函数，而柯西中值定理处理的对象是两个函数，如果结论中有两个函数，形式与柯西中值定理的形式类似，这时就要想到我们的柯西中值定理。

5. 积分中值定理的加强版若在定理证明中应用，必须先证明。

其次对于中值定理证明一般分为两大类题型：第一应用罗尔定理证明，也可又分为两小类：证明结论简单型和复杂型，简单型一般有证明f'(ξ)=0，f'(ξ)=k (k为任意常数)，f'(ξ1)=g'(ξ2)，f''(ξ)=0，f''(ξ)=g''(ξ)，像这样的结论一般只需要找罗尔定理的条件就可以了，一般罗尔定理的前两个条件题目均告知，只是要需找两个不同点的函数值相等，需找此条件一般会运用闭区间连续函数的性质、积分中值定理、拉格朗日中值定理、极限的性质、导数的定义等知识点。复杂型就是结论比较复杂，需要建立辅助函数，再使辅助函数满足罗尔定理的条件。辅助函数的建立一般借助于解微分方程的思想。第二就是存在两个点使之满足某表达式。这样的题目一般利用拉格朗日中值定理和柯西中值定理，处理思想把结论中相同字母放到等是一侧首先处理。

最后希望同学们仔细研究这块内容的历年试题，通过研究真正的把处理方法转化为自己的，跨考教育祝大家考研成功!

考研复习已经进入冲刺阶段，对于已经经过考研数学系统复习的考生，但做题有所欠缺的考生，不用紧张，跨考杨超老师为了帮助想直击数学分数130+的考生带来了福音，直击核心考点，透视历年试题，把握复习方向，强化基础知识，熟悉考研数学命题及考察形式，培养正确的解题思路，掌握基本的解题方法。

(实习编辑：刘佰万)