2020考研数学冲刺：二元隐函数极值求解_应用心理学考研
2019-03-28 09:34
来源：新东方网整理
作者：
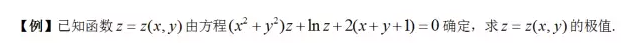大家知道，求二元函数极值的步骤：
1.找驻点;
2.分别求驻点处A,B,C;
3.求出极值。
但这类问题，第一步驻点就会遇到麻烦，涉及到二元隐函数方程求偏导，这里我们一般有两种方法。
一、直接对方程两边分别关于变量x,y求导，z看作x,y的函数;
二、隐函数存在定理，也即公式法计算一阶偏导数。
为了后续计算方便，建议大家用第一种方法求导，同时令一阶偏导数为0，可以直接找出驻点。
接下来的工作，就需要求二阶偏导，但注意到我们只要找出ABC就够了，不需要具体的二阶偏导函数，所以接下来的步骤：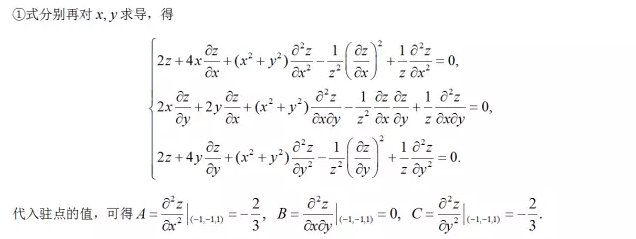
此时，若去求二阶偏导函数工程巨大，因为这道题会浪费掉大量的时间，你成功掉入出题人的陷进。
涉及到隐函数求二阶导问题，不论一元函数还是二元函数，基本都只考它们在一点处取值，只需：求而不解，代入法就能轻松化解计算量巨大的尴尬，你们，GET到了吗?
解答：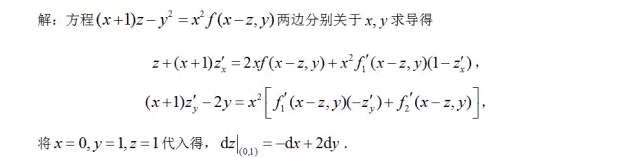
新东方重庆学校微信(微信号：xdf_cq)
最新考试资讯、教育新闻，请扫一扫二维码，关注我们的官方微信!
版权及免责声明
①凡本网注明"稿件来源：新东方"的所有文字、图片和音视频稿件，版权均属新东方教育科技集团（含本网和新东方网） 所有，任何媒体、网站或个人未经本网协议授权不得转载、链接、转贴或以其他任何方式复制、发表。已经本网协议授权的媒体、网站，在下载使用时必须注明"稿件来源：新东方"，违者本网将依法追究法律责任。
② 本网未注明"稿件来源：新东方"的文/图等稿件均为转载稿，本网转载仅基于传递更多信息之目的，并不意味着赞同转载稿的观点或证实其内容的真实性。如其他媒体、网站或个人从本网下载使用，必须保留本网注明的"稿件来源"，并自负版权等法律责任。如擅自篡改为"稿件来源：新东方"，本网将依法追究法律责任。
③ 如本网转载稿涉及版权等问题，请作者见稿后在两周内速来电与新东方网联系，电话：010-60908555。
在线咨询
课程预约